Regularization in the context of machine learning refers to a collection of strategies that help the machine learn more than solely memorize. In the simplest sense, ‘regularization’ indicates a set of techniques that regularizes learning from features for traditional algorithms or neurons in the case of neural network algorithms. Regularization is one of the major & most important concepts of machine learning. Regularization in machine learning prevents the model from overfitting. It basically reduces or regularizes the coefficient of features towards zero.

As mentioned above, regularization in machine learning, refers to a set of techniques that help the machine to learn more than just memorize. Before we explore the concept of regularization in detail, let’s discuss what the terms ‘learning’ and ‘memorizing’ mean from the perspective of machine learning.

When you train a machine learning model, and it is able to deliver accurate results on training data, but provides relatively poor results on unseen data or test dataset, you can say your model is memorizing more than generalizing.

Let’s say you are doing a cat vs dog classification and your trained model delivers 96% accuracy on training data, but when you run the same model using test dataset you get 85% accuracy on that data set – your model is memorizing more than generalizing

Let’s take a real-world scenario. Assume, an e-commerce company wishes to build a model to predict if the user would buy a product or not, given his/her usage history for last 7 days, and use the data for better decision making for retargeted digital advertisements. The usage history may include the number of pages visited, total time spent, the number of searches done, average time spent, page revisits, and more.

They build a model and it delivers accurate results on existing data but when they try to predict with unseen data, it doesn’t deliver a good result. Here, it can be concluded that the model does more of memorization than learning.

So what’s really happening with the above examples? One strong possibility is that the model has an overfitting problem, which results in relatively poor performance on unseen data. So essentially, memorizing is taking place here and not learning.

In general, if your model has a significant difference between evaluation metrics for training dataset and testing dataset, then it is said to have an overfitting problem.

Now that we have explored the concepts of memorizing, learning, and overfitting, let’s move to regularization and regularization techniques.

Regularization

The term ‘regularization’ refers to a set of techniques that regularizes learning from particular features for traditional algorithms or neurons in the case of neural network algorithms.

It normalizes and moderates weights attached to a feature or a neuron so that algorithms do not rely on just a few features or neurons to predict the result. This technique helps to avoid the problem of overfitting.

To understand regularization, let’s consider a simple case of linear regression. Mathematically, linear regression is stated as below:

y = w₀ + w₁x₁ + w₂x₂ + ….. + w_nx_n

where y is the value to be predicted;

x₁, x₂, …., x_n are features that decides the value of y;

w₀ is the bias;

w₁, w₂, ….., w_n are the weights attached to x₁, x₂, …., x_n relatively.

Now to build a model that accurately predicts the y value, we need to optimize above mentioned bias and weights.

To do so, we need to use a loss function and find optimized parameters using gradient descent algorithms and its variants.

The loss function called ‘the residual sum of square’ is mostly used for linear regression. Here’s what it looks like :

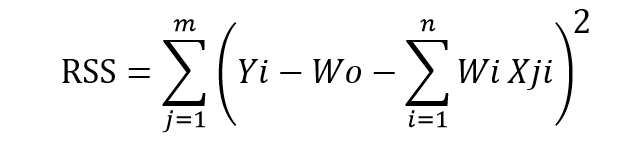
Next, we will learn bias (or intercept) and weights (also identified as parameters and coefficients) using the optimization algorithm (gradient descent) and data. If your dataset does have noise in it, it will face overfitting problem and learned parameters will not generalize well on unseen data.

To avoid this, you will need to regularize or normalize your weights for better learning.

There are three main regularization techniques, namely:

1. Ridge Regression (L2 Norm)
2. Lasso (L1 Norm)
3. Dropout

Ridge and Lasso can be used for any algorithms involving weight parameters, including neural nets. Dropout is primarily used in any kind of neural networks e.g. ANN, DNN, CNN or RNN to moderate the learning. Let’s take a closer look at each of the techniques.

Ridge Regression (L2 Regularization)

Ridge regression is also called L2 norm or regularization.

When using this technique, we add the sum of weight’s square to a loss function and thus create a new loss function which is denoted thus:

As seen above, the original loss function is modified by adding normalized weights. Here normalized weights are in the form of squares.

You may have noticed parameters λ along with normalized weights. λ is the parameter that needs to be tuned using a cross-validation dataset. When you use λ=0, it returns the residual sum of square as loss function which you chose initially. For a very high value of λ, loss will ignore core loss function and minimize weight’s square and will end up taking the parameters’ value as zero.

Now the parameters are learned using a modified loss function. To minimize the above function, parameters need to be as small as possible. Thus, L2 norm prevents weights from rising too high.

Lasso Regression (L1 Regularization)

Also called lasso regression and denoted as below:

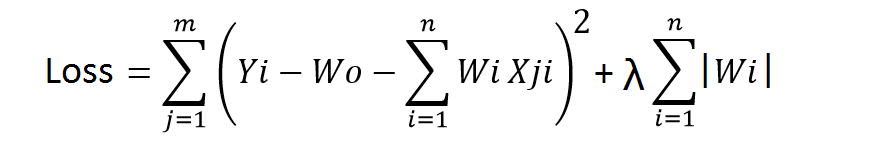
This technique is different from ridge regression as it uses absolute weight values for normalization. λ is again a tuning parameter and behaves in the same as it does when using ridge regression.

As loss function only considers absolute weights, optimization algorithms penalize higher weight values.

In ridge regression, loss function along with the optimization algorithm brings parameters near to zero but not actually zero, while lasso eliminates less important features and sets respective weight values to zero. Thus, lasso also performs feature selection along with regularization.

Dropout

Dropout is a regularization technique used in neural networks. It prevents complex co-adaptations from other neurons.

In neural nets, fully connected layers are more prone to overfit on training data. Using dropout, you can drop connections with 1-p probability for each of the specified layers. Where p is called keep probability parameter and which needs to be tuned.

With dropout, you are left with a reduced network as dropped out neurons are left out during that training iteration.

Dropout decreases overfitting by avoiding training all the neurons on the complete training data in one go. It also improves training speed and learns more robust internal functions that generalize better on unseen data. However, it is important to note that Dropout takes more epochs to train compared to training without Dropout (If you have 10000 observations in your training data, then using 10000 examples for training is considered as 1 epoch).

Along with Dropout, neural networks can be regularized also using L1 and L2 norms. Apart from that, if you are working on an image dataset, image augmentation can also be used as a regularization method.

For real-world applications, it is a must that a model performs well on unseen data. The techniques we discussed can help you make your model learn rather than just memorize.

Conclusion

Be it an over-fitting or under-fitting problem, it will lower down the overall performance of a machine learning model. To get the best out of machine learning models, you must optimize and tune them well. At eInfochips, we deliver machine learning services that help businesses optimize the utilization AI technology. We have machine learning capabilities across cloud, hardware, neural networks, and open source frameworks. Connect with our team to learn more about how machine learning can be useful to you.